问题
解答题
已知二次函数f（x）的二次项系数为a，且不等式f（x）＞﹣2x的解集为（1，3）．
（Ⅰ）若方程f（x）+6a=0有两个相等的根，求f（x）的解析式；
（Ⅱ）若f（x）的最大值为正数，求a的取值范围．
答案
解：（Ⅰ）∵f（x）+2x＞0的解集为（1，3）．f（x）+2x=a（x﹣1）（x﹣3），且a＜0．
因而f（x）=a（x﹣1）（x﹣3）﹣2x=ax2﹣（2+4a）x+3a．①
由方程f（x）+6a=0得ax2﹣（2+4a）x+9a=0．②
因为方程②有两个相等的根，
所以△=[﹣（2+4a）]2﹣4a·9a=0，即5a2﹣4a﹣1=0．
解得a=1或a=﹣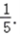
由于a＜0，舍去a=1．
将a=﹣
代入①得
f（x）的解析式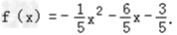
（Ⅱ）由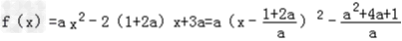
及a＜0，
可得f（x）的最大值为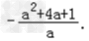
就由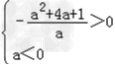
解得a＜﹣2﹣
或﹣2+
＜a＜0．
故当f（x）的最大值为正数时，
实数a的取值范围是