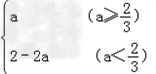解：（1）当4﹣3a=0，即a=时，f（x）=﹣2x+a为[0，1]上的减函数，

所以f（x）的最大值f（0）=a

（2）当4﹣3a＞0，即a时，函数图象是开口向上的抛物线，

因此函数在x∈[0，1]时的最大值为f（0）或f（1），

∵f（0）=a，f（1）=4﹣3a﹣2+a=2﹣2a，

∴f（0）﹣f（1）=3a﹣2

①当a=时，f（0）=f（1）=，函数的最大值是

②当a＜时，f（0）＜f（1），函数的最大值为f（1）=2﹣2a

③当＜a＜时，f（0）＞f（1），函数的最大值为f（0）=a

（3）当4﹣3a＜0，即a＞时，

函数图象是开口向下的抛物线，关于直线x=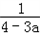对称

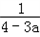∵＜0

∴f（x）在区间[0，1]上是减函数，函数的最大值为f（0）=a

综上所述，得f（x）的最大值为g（a）=