问题
解答题
幂函数g（x）=（m2﹣m﹣1）xm图象关于y轴对称，且函数f（x）=g（x）﹣2ax+1在x∈[﹣1，2]上的最小值为﹣2．
（1）求g（x）的解析式；
（2）求实数a的值．
答案
解：（1）由m2﹣m﹣1=1知m=2或m=﹣1．
①当m=2时，g（x）=x2，符合题意；
②当m=1时，g（x）=x﹣1，不符合题意，舍去．
∴g（x）=x2．
（2）f（x）=x2﹣2ax+1=（x﹣a）2+1﹣a2．
①当a＜﹣1时，f（x）min=f（﹣1）=2+2a=﹣2，
∴a=﹣2；
②当a＞2时，f（x）min=f（2）=5﹣4a=﹣2，
∴
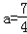，与a＞2矛盾，舍去；
③当﹣1≤a≤2时，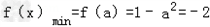
，
∴
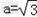或
，
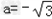又﹣1≤a≤2，
∴
．
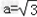综上，a=﹣2或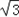
．
n 
n