问题
解答题
已知函数f（x）=ax2﹣2ax+3﹣b（a＞0）在[1，3]有最大值5和最小值2，求a、b的值．
答案
解：∵f（x）=ax2﹣2ax+3﹣b（a＞0）的对称轴x=1，[1，3]是f（x）的递增区间，
∴f（x）max=f（3）=5，即3a﹣b+3=5
∴f（x）min=f（1）=2，即﹣a﹣b+3=2
∴
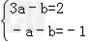
得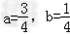
故a=
，b=
．
搜题请搜索小程序“爱下问搜题”
已知函数f（x）=ax2﹣2ax+3﹣b（a＞0）在[1，3]有最大值5和最小值2，求a、b的值．
解：∵f（x）=ax2﹣2ax+3﹣b（a＞0）的对称轴x=1，[1，3]是f（x）的递增区间，
∴f（x）max=f（3）=5，即3a﹣b+3=5
∴f（x）min=f（1）=2，即﹣a﹣b+3=2
∴
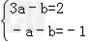
得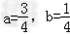
故a=，b=．