问题
解答题
设fk（n）为关于n的k（k∈N）次多项式．数列{an}的首项a1=1，前n项和为Sn。对于任意的正整数n，an+Sn=fk（n）都成立。
（1）若k=0，求证：数列{an}是等比数列；
（2）试确定所有的自然数k，使得数列{an}能成等差数列。
答案
解：（1）若k=0，则
为常数，
不妨设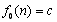
（c为常数），
因为
恒成立，
所以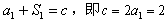
，
而且当n≥2时，
， ①
， ②
①-②得
，
若an=0，则
，…，a1=0，与已知矛盾，
所以
，
故数列{an}是首项为1，公比为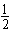
的等比数列；
（2）(i)若k=0，由（1）知，不符题意，舍去；
(ii)若k=1，设
（b，c为常数），
当n≥2时，
， ③
， ④
③-④得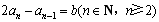
，
要使数列{an}是公差为d（d为常数）的等差数列，必须有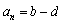
（常数），
而a1=1，
故{an}只能是常数数列，通项公式为an=1（n∈N*），
故当k=1时，数列{an}能成等差数列，其通项公式为an=1（n∈N*），
此时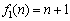
；
(iii)若k=2，设
（a≠0，a，b，c是常数），
当n≥2时，
， ⑤
， ⑥
⑤-⑥得
，
要使数列{an}是公差为d（d为常数）的等差数列，
必须有
，且d=2a，
考虑到a1=1，
所以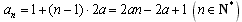
，
故当k=2时，数列{an}能成等差数列，其通项公式为
，
此时
（a为非零常数）；
(iv)当k≥3时，若数列{an}能成等差数列，则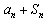
的表达式中n的最高次数为2，故数列{an}不能成等差数列；
综上得，当且仅当k=1或2时，数列{an}能成等差数列。