解：（1）∵函数f（x）=|x﹣a|为偶函数，

∴对任意的实数x，f（﹣x）=f（x）成立即|﹣x﹣a|=|x﹣a|，

∴x+a=x﹣a恒成立，或x+a=a﹣x恒成立

∵x+a=a﹣x不能恒成立

∴x+a=x﹣a恒成立，得a=0．

（2）当a＞0时，|x﹣a|﹣ax=0有两解，

等价于方程（x﹣a）²﹣a²x²=0在（0，+∞）上有两解，

即（a²﹣1）x²+2ax﹣a²=0在（0，+∞）上有两解，

令h（x）=（a²﹣1）x²+2ax﹣a²，

因为h（0）=﹣a²＜0，

所以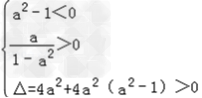 ，故0＜a＜1；

同理，当a＜0时，得到﹣1＜a＜0；

当a=0时，f（x）=|x|=0=g（x），显然不合题意，舍去．

综上可知实数a的取值范围是（﹣1，0）∪（0，1）．

（3）令F（x）=f（x）·g（x）

①当0＜a≤1时，则F（x）=a（x²﹣ax），

对称轴 ，函数在[1，2]上是增函数，

所以此时函数y=F（x）的最大值为4a﹣2a²．

②当1＜a≤2时， ，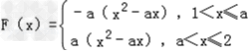

对称轴 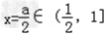，所以函数y=F（x）在（1，a]上是减函数，

在[a，2]上是增函数，F（1）=a²﹣a，F（2）=4a﹣2a²，

1）若F（1）＜F（2），即 ，此时函数y=F（x）的最大值为4a﹣2a²；

2）若F（1）≥F（2），即 ，此时函数y=F（x）的最大值为a²﹣a．

③当2＜a≤4时，F（x）=﹣a（x²﹣ax）

对称轴 ，此时 ，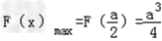

④当a＞4时，对称轴 ，此时 ．

综上可知，函数y=F（x）在区间[1，2]上的最大值