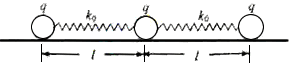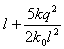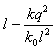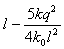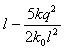问题
填空题
| 以下四个关于圆锥曲线的命题中: ①设A、B为两个定点,k为非零常数,若||PA|-|PB||=k,则动点P的轨迹为双曲线; ②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若
③抛物线x=ay2(a≠0)的焦点坐标是(
④曲线
其中真命题的序号为______写出所有真命题的序号. |
答案
①因为双曲线的定义中要求k<|AB|故①不成立
②设定圆C的方程为x2+y2=9,点A(3,0),B(a,b),点P(x,y),
则由
=OP 1 2
+OA 1 2
得动点P为动弦AB的中点,所以有OB
⇒x= a+3 2 y= b 2 a=2x-3 b=2y
又因为点B在圆上所以有(2x-3)2+(2y)2=9
即动点P的轨迹为圆.所以②为假命题.
③先把抛物线转化为标准形式y2=
x,a>0,2p=1 a
,1 a
=p 2
,焦点坐标是(1 4a
,0);1 4a
a<0,2p=-
,1 a
=-p 2
,焦点坐标是(1 4a
,0);③为真命题.1 4a
④因为曲线
-x2 16
=1的焦点为(5,0)(-5,0).y2 9
而由曲线
+x2 35-λ
=1中λ<35且λ≠10知表示的是a2=35-λ,b2=10-λ,c2=25,的椭圆,所以焦点为(5,0)(-5,0).即④为真命题.y2 10-λ
故答案为 ③④.