问题
解答题
已知函数f（x）=﹣x2+2ax﹣1，x∈[﹣2，2]，
（1）当a=1时，求f（x）的最大值与最小值；
（2）求实数a的取值范围，使函数f（x）在[﹣2，2]上是减函数；
（3）求函数f（x）的最大值g（a），并求g（a）的最小值．
答案
解：（1）当a=1时，f（x）=﹣x2+2x﹣1=﹣（x﹣1）2，
∵﹣2≤x≤2
∴f（x）min=f（﹣2）=﹣9，f（x）max= f（1）=0
（2）∵f（x）=﹣x2+2ax﹣1=﹣（x﹣a）2+a2﹣1
∴当x≥a时，f（x）为减函数，当x≤a时，f（x）为增函数
∴要使f（x）在[﹣2，2]上为减函数，则[﹣2，2]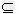
[a，+∞），
解得：a≤﹣2，
∴a的取值范围是（﹣∞，﹣2]
（3）由f（x）=﹣x2+2ax﹣1=﹣（x﹣a）2+a2﹣1（﹣2≤x≤2）
∴当﹣2≤a≤2时，g（a）=f（a）=a2﹣1
当a＜﹣2时，g（a）=f（﹣2）=﹣4a﹣5
当a＞2时，g（a）=f（2）=4a﹣5
∴g（a）=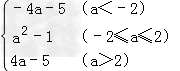 
∴当﹣2≤a≤2时，g（a）=a2﹣1，
∴﹣1≤g（a）＜3 当a＞2时，g（a）=4a﹣5，
∴g（a）＞3 当a＜﹣2时，g（a）=﹣4a﹣5，
∴g（a）＞3
综上得：g（a）≥﹣1