问题
解答题
已知奇函数f（x）的定义域是R，且f（x）=f（1﹣x），当0≤x≤ 时，f（x）=x﹣x2．
（1）求证：f（x）是周期函数；
（2）求函数f（x）在区间[1，2]上的解析式；
（3）求函数f（x）的值域．
答案
解：（1）f（x+2）=f（1﹣（x+2））=f（﹣x﹣1）=﹣f（x+1）=﹣f（1﹣（x+1））=﹣f（﹣x）=f（x），
所以f（x）是周期为2的函数．
（2）∵当x∈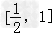
时，f（x）=f（1﹣x）=（1﹣x）﹣（1﹣x）2=x﹣x2，
∴x∈[0，1]时，f（x）=x﹣x2
∴当x∈[1，2]时，f（x）=f（x﹣2）=﹣f（2﹣x）=（2﹣x）2﹣（2﹣x）=x2﹣3x+2．
∴当x∈[1，2]时，f（x）=x2﹣3x+2．
（3）由函数是以2为周期的函数，
故只需要求出一个周期内的值域即可，由（2）知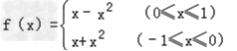
，
故在[﹣1，1]上函数的值域是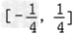 
，
故值域为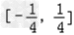
．