（1）扇形弧长为20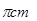

（2）

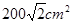
（过程略，酌情给分）

本题考查扇形的面积公式和弧长公式，并考查平面图形与立体图形之间的联系，学生必需了解圆锥轴截面的知识。

解：（1）先根据扇形的面积公式，把已知条件代入可求出扇形的半径R=30cm，然后再根据弧长公式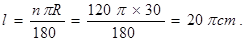

（2）若把此扇形卷成一个圆锥后，扇形的半径为圆锥的母线长，圆锥的底面周长为扇形的弧长20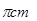，根据圆的周长公式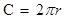，得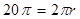由此可知r=10cm,再由圆锥的母线、高线、底面半径组成直角三角形，根据勾股定理可求出圆锥的高为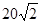cm，则圆锥的轴截面的面积是以圆锥的底面直径、两条母线为三边的等腰三角形，则其面积为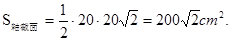：(每一小问4分，也可根据实际酌情给分)