问题
解答题
设数列{an}满足：ban-2n=(b-1)Sn，
（Ⅰ）当b=2时，求证：{an-n·2n-1}是等比数列；
（Ⅱ）求an的通项公式．
答案
解：由题意，在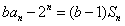
中，令n=1，得
，a1=2，
由
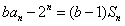，得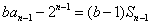
，
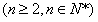两式相减得：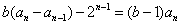
，
即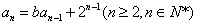
， ①
（Ⅰ）当b=2时，由①知，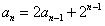
，
于是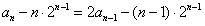
，
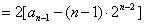
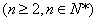又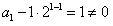
，
所以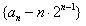
是首项为1，公比为2的等比数列．
（Ⅱ）当b=2时，由（Ⅰ）知，
，即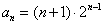
；
当b≠2时，由①：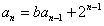
，
两边同时除以2n得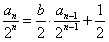
，
可设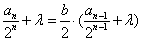
，②
展开②得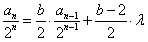
，
与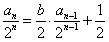
比较，得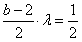
，
∴
，
∴
，
∴
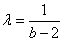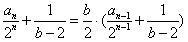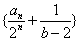是等比数列，公比为
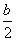，首项为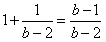
，
∴
，
∴
，
∴
。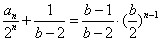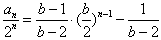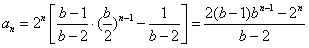