问题
解答题
已知数列{an}满足an+1=2an+n+1(n=1,2,3,…)。
(1)若{an}是等差数列,求其首项a1和公差d;
(2)证明{an}不可能是等比数列;
(3)若a1=-1,求{an}的通项公式以及前n项和公式。
答案
解:(1)因为{an}是等差数列,设其首项为a1,公差为d,
则an=a1+(n-1)d,
于是有a1+nd=2[a1+(n-1)d]+n+1,
整理得a1+nd=(2a1-2d+1)+(2d+1)n,
因此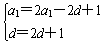 ,
,
解得a1=-3,d=-1。
(2)证明:假设{an}是等比数列,设其首项为a1,
则a2=2a1+2,a3=2a2+3=4a1+7,
于是有(2a1+2)2=a1(4a1+7),
解得a1=-4,
于是公比q=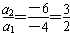 ,
,
这时a4=a1q3=(-4)·(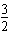 )3=-
)3=-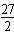
但事实上,a4=2a3+4=8a1+18=-14,二者矛盾,
所以{an}不是等比数列。
(3)由an+1=2an+n+1可得an+1+(n+1)+2=2(an+n+2),
所以数列{an+n+2}是一个公比为2的等比数列,其首项为(a1+1+2)=-1+1+2=2,
于是an+n+2=2·2n-1=2n
故an=2n-n-2,
于是{an}的前n项和公式
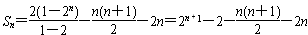 。
。
