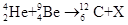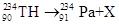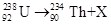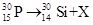问题
解答题
设数列{an}的前n项和为Sn，且Sn=4an-3（n=1，2，…）。
（1）证明：数列{an}是等比数列；
（2）若数列{bn}满足bn+1=an+bn（n=1，2，…），b1=2，求数列{bn}的通项公式。
答案
解：（1）证明：因为Sn=4an-3（n=1，2，…），
则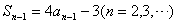
所以当n≥2时，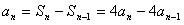
整理得
由Sn=4an-3，令n=1，得a1=4a1-3，解得a1=1
所以{an}是首项为1，公比为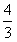
的等比数列。
（2）解：因为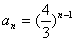
由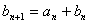
（n=1，2，…），得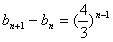
由累加得
bn=b1+（b2-b1）+（b3-b2）+…+（bn-bn-1）
当n=1时也满足，所以
。