问题
填空题
f（x）=|x2-4x+3|-a有三个零点，则实数a所构成的集合为 ______
答案
因为f（x）=|x2-4x+3|-a有三个零点，
就是函数y=|x2-4x+3|与y=a的图象有三个交点，
又因为y=|x2-4x+3|=
，x2-4x+3 x≥3，x≤1 -x2+4x-3 1＜x＜3
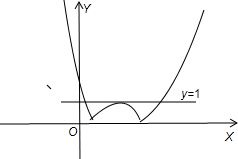
画出对应图象．如图得，当y=a=1时，符合要求．
故答案为{1}．
搜题请搜索小程序“爱下问搜题”