问题
解答题
已知函数f(x)=x2-2|x|-1
(1)判断f(x)的奇偶性;
(2)画出f(x)的图象;
(3)指出f(x)的单调区间.
答案
(1)∵f(-x)=(-x)2-2|-x|-1=x2-2|x|-1=f(x)
∴f(x)是偶函数(4分)
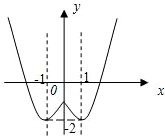
(2)函数的解析式可化为:
f(x)=
(7分)x2-2x-1,x≥0 x2+2x-1,x<0
其图象如图所示:
(3)由(2)中图象可得:
函数的递增区间为[-1,0],[1,+∞)
递减区间为(-∞,-1],[0,1](15分)
