解（1）θ=

π

6

时，f(x)=x2+x-1=(x+

1

2

)2-

5

4

由x∈[-

3

2

，

1

2

]，当x=-

1

2

时，f（x）有最小值为-

5

4

当x=

1

2

时，f（x）有最大值为-

1

4

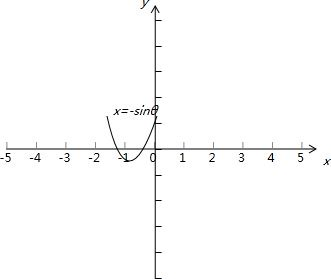
（2）f（x）=x²+2xsinθ-1的图象的对称轴为x=-sinθ，

由于f（x）在x∈[-

3

2

，

1

2

]上是单调增函数      

所以-sinθ≤-

3

2

，

即sinθ≥

3

2

，又∵θ∈[0，2π）

所求θ的取值范围是[

π

3

，

2π

3

]．