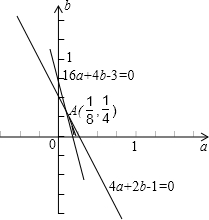
（1）设g（x）=f（x）-x=ax²+（b-1）x+1，

∵a＞0，

∴由条件x₁＜2＜x₂＜4，

得g（2）＜0，g（4）＞0．即

4a+2b-1＜0 16a+4b-3＞0

由可行域可得

b

a

＜2，∴x0=-

b

2a

＞-1．

（2）由g（x）=ax²+（b-1）x+1=0，知x1x2=

1

a

＞0，故x₁与x₂同号．

①若0＜x₁＜2，则x₂-x₁=2（负根舍去），

∴x₂=x₁+2＞2．

∴

g(2)＜0 g(4)＞0

，即

4a+2b-1＜0 16a+4b-3＞0

⇒b＜

1

4

；

②若-2＜x₁＜0，则x₂=-2+x₁＜-2（正根舍去），

g(-2)＜0 g(-4)＞0

，即

4a-2b+3＜0 16a-4b+5＞0

⇒b＞

7

4

．

综上，b的取值范围为b＜

1

4

或b＞

7

4

．