问题
选择题
⊿ABC中，∠C=90°，AB=5，BC=4，以A为圆心，以3为半径，则点C与⊙A的位置关系为（ ）
A．点C在⊙A内
B．点C在⊙A上
C．点C在⊙A外
D．点C在⊙A上或点C在⊙A外
答案
答案：B
由勾股定理得：AC=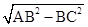
=
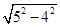=3，
∵AC=3=3，
∴点C与⊙A的位置关系是点C在⊙A上，
故答案为点C在⊙A上．故答案选B．
搜题请搜索小程序“爱下问搜题”
⊿ABC中，∠C=90°，AB=5，BC=4，以A为圆心，以3为半径，则点C与⊙A的位置关系为（ ）
A．点C在⊙A内
B．点C在⊙A上
C．点C在⊙A外
D．点C在⊙A上或点C在⊙A外
答案：B
由勾股定理得：AC=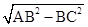==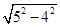3，
∵AC=3=3，
∴点C与⊙A的位置关系是点C在⊙A上，
故答案为点C在⊙A上．故答案选B．