问题
填空题
以椭圆
|
答案
∵椭圆
+x2 9
=1长轴两个端点坐标为(0,5)和(0,-5),y2 25
焦点坐标为(0,4)和(0,-4),
∴双曲线方程设为
-y2 a2
=1,x2 b2
c=5,
=4,a2 c
解得a2=20,b2=5,
∴双曲线方程为
-y2 20
=1,x2 5
其淅近线方程为y=±2x,
∴双曲线的渐近线的斜率k=±2.
故答案为:±2.
以椭圆
|
∵椭圆
+x2 9
=1长轴两个端点坐标为(0,5)和(0,-5),y2 25
焦点坐标为(0,4)和(0,-4),
∴双曲线方程设为
-y2 a2
=1,x2 b2
c=5,
=4,a2 c
解得a2=20,b2=5,
∴双曲线方程为
-y2 20
=1,x2 5
其淅近线方程为y=±2x,
∴双曲线的渐近线的斜率k=±2.
故答案为:±2.
(14分)
I.仅用下列装置,检验木炭和浓硫酸反应产生的混和气体中含有SO2和CO2。在下列表格中填写对应的药品和实验现象。
| 实验装置 | 检验气体 | 试剂名称 | 实验现象 |
| A | SO2 | ||
| B | CO2 |
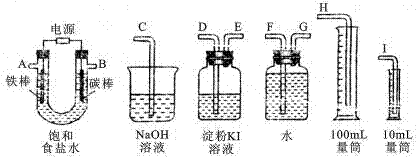
(1)将上面各仪器连成一整套装置,各种仪器接口的连接顺序(填编号)是:A接______________,B接______________。
(2)请写出铁棒电极上发生的电极反应式__________________________。
(3)能说明氯气具有氧化性的实验现象是_______________________________。
(4)若U管中装入的饱和食盐水为50mL(电解前后溶液体积变化可忽略),当收集到的氢气为5.6mL(标准状况)时停止通电,摇匀U型管内的溶液,取20.00mL该溶液于锥形瓶内,用0.01mol/L的盐酸滴定时,滴定管起始读数为1.00mL,滴定终点时,滴定管的读数为_______ mL。