问题
解答题
已知函数f（x）=x2-2ax-1在区间[0，2]上的最大值为g（a），最小值为h（a）．（a∈R）
（1）求g（a）和h（a）；
（2）作出g（a）和h（a）的图象，并分别指出g（a）的最小值和h（a）的最大值各为多少？
答案
解（1）f（x）=x2-2ax-1=（x-a）2-（1+a2）
∵x∈[0，2]
①当a≤0时，g（a）=f（2）=3-4a，h（a）=f（0）=-1
②当0＜a≤1时，g（a）=f（2）=3-4a，h（a）=f（a）=-（1+a2）
③当1＜a≤2时，g（a）=f（0）=-1，h（a）=f（a）=-（1+a2）
④当a≥2时，g（a）=f（0）=-1，h（a）=f（2）=3-4a
综上可得，g（a）=3-4a，a≤1 -1，a＞1
h（a）=-1，a≤0 -(1+a2)，0＜a＜2 3-4a，a≥2
（2）函数g（a）与h（a）的图象如图所示
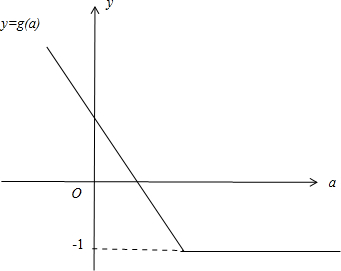
由图象可知，y=g（a）的最小值为-1
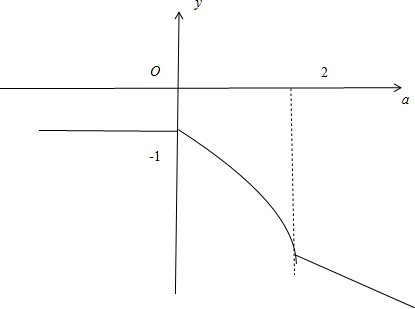
由图象知，函数y=h（a）的最大值为-1