问题
填空题
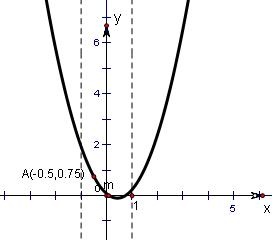
若函数f(x)=x2+(2m-1)x+m在区间[-1,1]内有零点,则m的取值范围是______.
答案
由于f(x)=x2+(2m-1)x+m=x2-x+m(2x-1),故它的图象一定过点(
,1 2
),3 4
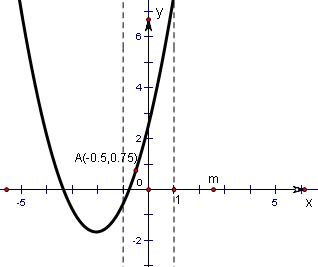
当f(x)在[-1,1]上有一个零点时,
此时①
,或 ②f(-1)≤0或f(1)≤0成立.△=(2m-1)2-4m=0 -1≤
≤11-2m 2
解①得 m=1-
,解②得 m<0或m≥2.3 2
当f(x)在[-1,1]上有两个零点时,此时
,解得0≤m<1-△=(2m-1)2-4m>0 -1≤
≤11-2m 2 f(1)≥0 f(
)<01-2m 2
,3 2
综上可得,实数m的取值范围:m≥2或m≤1-
.3 2