答案：D

根据题意，设BF=BD=x，则CD=CE=11-x，AE=AF=10-x，列出等式11-x+10-x=7，求出x的值，再由切线长定理得出△BMN的周长是BD+BF即可．

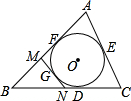
解：设BF=BD=x，

∵⊙O为△ABC的内切圆，且AB=10，BC=11，AC=7，

∴CD=CE=11-x，AE=AF=10-x，

∴11-x+10-x=7，

解得x=7，

∵MN切⊙O于点G，∴MF=MG，ND=NG，

∴△BMN的周长=BM+BN+MG+NG=BD+BF=2x=14，

故选D．

本题考查了切线长定理和三角形的内切圆．