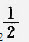问题
解答题
过点P(-4,0)的直线l与曲线C:x2+2y2=4交于A,B;求AB中点Q的轨迹方程.
答案
设A,B两点坐标为:(x1,y1),(x2,y2),设中点Q(x,y)
设直线l的方程为y=k(x+4),代入x2+2y2=2,得(1+2k2)x2+16k2x+32k2-4=0,
所以x1+x2=-
,∴x=-16k2 1+2k2
,y=8k2 1+2k2 4 1+2k2
消去参数可得(x+2)2+2y2=4
由△>0可得0≤k2<
,∴-1<x≤01 6
∴AB中点Q的轨迹方程为(x+2)2+2y2=4(-1<x≤0)

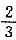 ]×[
]×[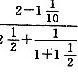 ]的值是()。
]的值是()。