问题
解答题
已知函数f(x)=x2-2|x|-1,(-3≤x≤3),
(Ⅰ)指出函数的奇偶性并画出其简图;
(Ⅱ)若y=a与函数f(x)的图象有两个交点求实数a的取值范围.
答案
(I)∵函数f(x)=x2-2|x|-1,(-3≤x≤3)的定义域关于原点对称,
且f(-x)=(-x)2-2|-x|-1=x2-2|x|-1=f(x)
故函数为偶函数,其简图如下图所示:
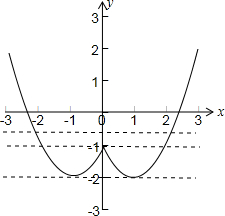
(II)由(I)中函数的简图可得
当a<-2时,y=a与函数f(x)的图象没有交点;
当a=-2时,y=a与函数f(x)的图象有两个交点;
当-2<a<-1时,y=a与函数f(x)的图象有四个交点;
当a=-1时,y=a与函数f(x)的图象有三个交点;
当a>-1时,y=a与函数f(x)的图象有两个交点;
故满足条件的实数a的取值范围是,a>-1或a=-2
