问题
解答题
工厂有一批长3dm、宽2dm的矩形铁片，为了利用这批材料，在每一块上裁下一个最大的圆铁片⊙O1之后（如图所示），再在剩余铁片上裁下一个充分大的圆铁片⊙O2．
小题1:（1）求⊙O1、⊙O2的半径r1、r2的长；
小题2:（2）能否在剩余的铁片上再裁出一个与⊙O2同样大小的圆铁片？为什么？
答案
小题1:⑴如图，矩形ABCD中，AB= 2r1=2dm，即r1="1dm. " ………………………………1分
BC=3dm，⊙O2应与⊙O1及BC、CD都相切.
连结O1 O2，过O1作直线O1E∥AB，过O2作直线O2E∥BC，则O1E⊥O2E.
在Rt△O1 O2E中，O1 O2=r1+ r2，O1E= r1– r2，O2E=BC–(r1+ r2).
由 O1 O22= O1E2+ O2E2，
即（1+ r2)2 = (1– r2)2+(2– r2)2.
解得，r2= 4±2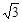
. 又∵r2<2,
∴r1=1dm， r2=（4–2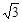）dm.
小题2:⑵不能.
∵r2=（4–2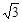）> 4–2×1.75=
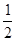(dm),
即r2>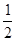dm.，又∵CD=2dm，
∴CD<4 r2，故不能再裁出所要求的圆铁片