问题
填空题
已知函数f(x)=-x2+x,x∈[-2,1],则函数f(x)的值域为 [-6,
|
答案
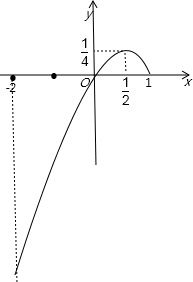
因为二次函数的对称轴x=-
=-b 2a
=1 -2
,又x∈[-2,1],1 2
所以二次函数的顶点坐标能取到,则f(x)的最大值为
=4ac-b2 4a
=0-12 -4
,1 4
根据图象可知:f(x)的最小值为f(-2)=-4-2=-6,
所以函数f(x)的值域为:[-6,
].1 4
故答案为:[-6,
]1 4
