| 已知平面内一动点P到定点F(2,0)的距离与点P到y轴的距离的差等于2. (Ⅰ)求动点P的轨迹C的方程; (Ⅱ)过点F作倾斜角为60°的直线l与轨迹C交于A(x1,y1),B(x2,y2)(x1<x2)两点,O为坐标原点,点M为轨迹C上一点,若向量
|
(Ⅰ)∵平面内一动点P到定点F(2,0)的距离与点P到y轴的距离的差等于2,
∴P到F的距离等于P到直线x=-2的距离
∴圆心P的轨迹为以F(2,0)为焦点的抛物线
∴轨迹C的方程为y2=8x;
(Ⅱ)设M(x,y),则直线l的方程为y=
(x-2)3
代入y2=8x得:3x2-20x+12=0
∴x1=
,x2=62 3
∴y1=-
,y2=44 3 3 3
∵
=OM
+λOA
,OB
∴x=x1+λx2,y=y1+λy2,
∴x=
+6λ,y=-2 3
+44 3 3
λ3
∵点M为轨迹C上一点,∴y2=8x,
∴(-
+44 3 3
λ)2=8(3
+6λ)2 3
∴3λ2-5λ=0
∴λ=
或0.5 3

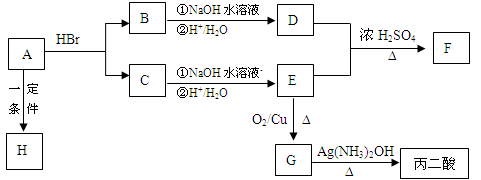
 ①上述化合物中的含氧官能团是(写名称) 、 、 、
①上述化合物中的含氧官能团是(写名称) 、 、 、  ;
; ;
;