问题
填空题
在半径为2的⊙O中，弦AB的长为2，则弦AB所对的圆周角的度数为
答案
30度或150度
如图，弦AB所对的圆周角为∠C，∠D，
 |
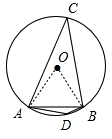连接OA、OB，
因为AB=OA=OB=2，
所以，∠AOB=60°，
根据圆周角定理知，∠C="1" 2 ∠AOB=30°，
根据圆内接四边形的性质可知，∠D=180°-∠C=150°，
所以，弦AB所对的圆周角的度数30°或150°
搜题请搜索小程序“爱下问搜题”