问题
解答题
已知在数列{an}中,a1=-1,且an=3an-1-2n+3(n≥2,n∈N+).
(Ⅰ)求a2,a3,并证明数列{an-n}是等比数列;
(Ⅱ)求a1+a2+…+an的值.
答案
(Ⅰ)∵a1=-1,且an=3an-1-2n+3,∴a2=-3-4+3=-4,a3=-12-6+3=-15
∵an=3an-1-2n+3,∴an-n=3[an-1-(n-1)]
∴数列{an-n}是以-2为首项,3为公比的等比数列;
(Ⅱ)由(Ⅰ)知,an-n=(-2)•3n-1
∴an=n-2•3n-1
∴a1+a2+…+an=
-3n+1.n(1+n) 2

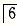 残根,根尖瘘管挤压无脓,治疗设计为局麻下拔除,麻醉顺利,10min后检查,麻醉效果良好,开始操作,术中患者觉疼痛但可耐受,其后自诉头晕,胸闷恶心,检查患者面色苍白,四肢冷而无力,脉快而弱。
残根,根尖瘘管挤压无脓,治疗设计为局麻下拔除,麻醉顺利,10min后检查,麻醉效果良好,开始操作,术中患者觉疼痛但可耐受,其后自诉头晕,胸闷恶心,检查患者面色苍白,四肢冷而无力,脉快而弱。