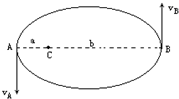
已知椭圆C:x2+
(Ⅰ)若l与x轴相交于点P,且P为AM的中点,求直线l的方程; (Ⅱ)设点N(0,
|
(Ⅰ)设A(x1,y1),
因为P为AM的中点,且P的纵坐标为0,M的纵坐标为1,
所以
=0,解得y1=-1,(1分)y1+1 2
又因为点A(x1,y1)在椭圆C上,
所以x12+
=1,即x12+ y12 4
=1,解得x1=±1 4
,3 2
则点A的坐标为(
,-1)或(-3 2
,-1),3 2
所以直线l的方程为4
x-3y+3=0,或43
x+3y-3=0.3
(Ⅱ)设A(x1,y1),B(x2,y2),
则
=(x1,y1-NA
),1 2
=(x2,y2-NB
),1 2
所以
+NA
=(x1+x2,y1+y2-1),NB
则|
+NA
| =NB
,(x1+ x2)2+(y1+y2-1)2
当直线AB的斜率不存在时,
其方程为x=0,A(0,2),B(0,-2),此时|
+NA
|=1;NB
当直线AB的斜率存在时,设其方程为y=kx+1,
由题设可得A、B的坐标是方程组
的解,y=kx+1 x2+
=1y2 4
消去y得(4+k2)x2+2kx-3=0,
所以△=(2k)2+12(4+k2)>0,x1+x2=
,-2k 4+k2
则y1+y2=(kx1+1)+(kx2+1)=
,8 4+k2
所以|
+NA
|2=(NB
)2+(-2k 4+k2
-1)28 4+k2
=
+1≤1,-12k2 (4+ k2)2
当k=0时,等号成立,即此时|
+NA
|取得最大值1.NB
综上,当直线AB的方程为x=0或y=1时,|
+NA
|有最大值1.NB