问题
解答题
设数列{an}的首项a1=a≠
(Ⅰ)求a2,a3; (Ⅱ)数列{bn}是否为等比数列,如果是,求出其通项公式;如果不是,请说明理由. |
答案
(Ⅰ)因为数列{an}的首项a1=a≠
,且an+1=1 4
,
an1 2 (n为偶数) an+ 1 4 (n为奇数)
所以,a2=a1+
=a+1 4
,a3=1 4
a2=1 2
a+1 2
.1 8
(Ⅱ)数列{an}的首项a1=a≠
,且an+1=1 4
,a3=
an1 2 (n为偶数) an+ 1 4 (n为奇数)
a+1 2
.1 8
∴a4=a3+
=1 4
a+1 2
,3 8
∴a5=
a4=1 2
a+1 4
,3 16
所以b1=a1-
=a-1 4
,b2=a3-1 4
=1 4
(a-1 2
),b3=a5-1 4
=1 4
(a-1 4
),1 4
猜想:{bn}是公比为
的等比数列.1 2
证明如下:
因为bn+1=a2n+1-
=1 4
a2n-1 2
=1 4
(a2n-1+1 2
)-1 4
=1 4
(a2n-1-1 2
)=1 4
bn,1 2
所以{bn}是首项为a-
,公比为1 4
的等比数列.1 2
故bn=(a-
)•(1 4
)n-1.1 2

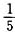 ,第二次读了剩余页数的
,第二次读了剩余页数的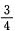 。这时,还有剩下35页,则原书有()页。
。这时,还有剩下35页,则原书有()页。