在数列{an}中,a1=3,an=-an-1-2n+1(n≥2且n∈N*).
(1)求a2,a3的值;
(2)证明:数列{an+n}是等比数列,并求{an}的通项公式;
(3)求数列{an}的前n项和Sn.
(1)∵a1=3,an=-an-1-2n+1(n≥2,n∈N*),
∴a2=-a1-4+1=-6,a3=-a2-6+1=1.
(2)∵
=an+n an-1+(n-1)
=(-an-1-2n+1)+n an-1+n-1
=-1,-an-1-n+1 an-1+n-1
∴数列{an+n}是首项为a1+1=4,公比为-1的等比数列.
∴an+n=4•(-1)n-1,即an=4•(-1)n-1-n,
∴{an}的通项公式为an=4•(-1)n-1-n(n∈N*).
(3)∵{an}的通项公式为an=4•(-1)n-1-n(n∈N*),
所以Sn=
ak=n 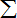
k-1
[4•(-1)k-1-k]=n 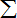
k-1
[4•(-1)k-1-n 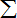
k-1
kn 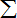
k-1
=4×
-1-(-1)n 1-(-1) n(n+1) 2
=2[1-(-1)n]-
(n2+n)1 2
=-
-2(-1)n.n2+n-4 2
