问题
填空题
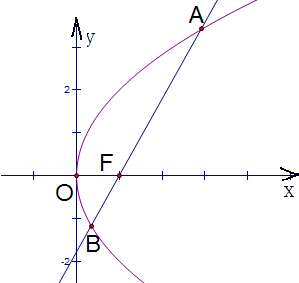
过抛物线y2=4x的焦点作倾斜角为
|
答案
根据抛物线y2=4x方程得:焦点坐标F(1,0),
直线AB的斜率为k=tan
=π 3 3
由直线方程的点斜式方程,设AB:y=
(x-1)3
将直线方程代入到抛物线方程当中,得:3(x-1)2=4x
整理得:3x2-10x+3=0
设A(x1,y1),B(x2,y2)
由一元二次方程根与系数的关系得:x1+x2= 10 3 x1x2=1
所以弦长|AB|=
|x1-x2|=1+k2 1+3
=(x1+x2)2-4x1x2 16 3
故答案为16 3