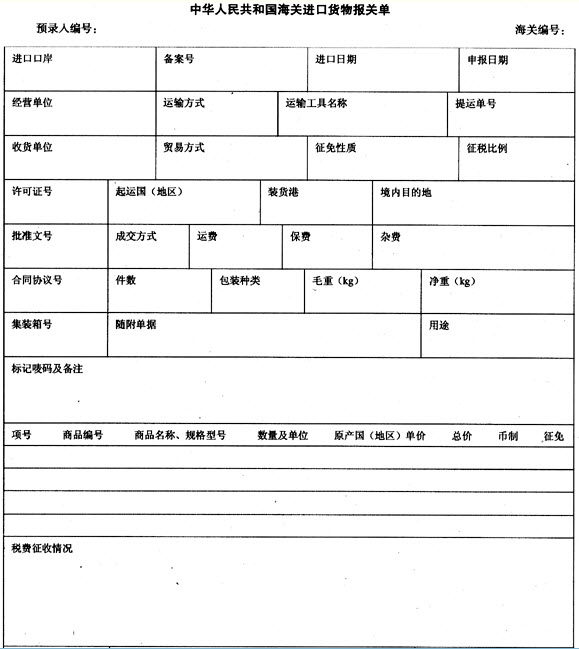
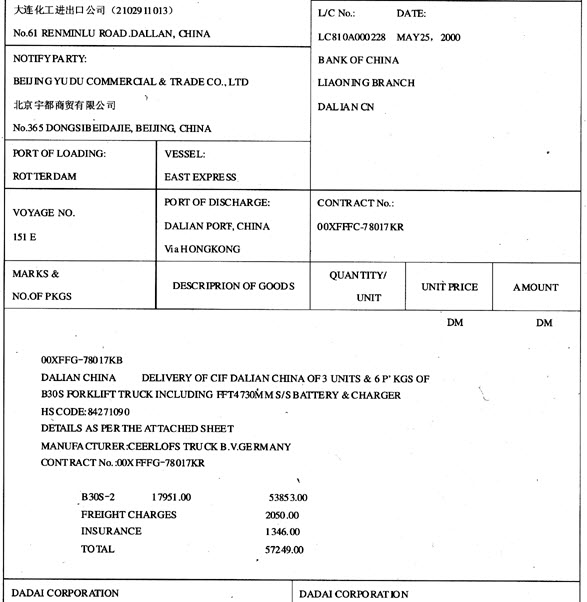
问题
解答题
在数列an中，a1=1，2an+1=(1+
（Ⅰ）证明数列{
（Ⅱ）令bn=an+1-
|
答案
（Ⅰ）由条件得
=an+1 (n+1)2
•1 2
，（2分）an n2
又n=1时，
=1，（3分）an n2
故数列{
}构成首项为1，公式为an n2
的等比数列．（4分）1 2
从而
=an n2
，即an=1 2n-1
．（6分）n2 2n-1
（Ⅱ）由bn=
-(n+1)2 2n
=n2 2n
（8分）2n+1 2n
得Sn=
+3 2
+… +5 22
⇒2n+1 2n
Sn=1 2
+3 22
+…+5 23
+2n-1 2n
，2n+1 2n+1
两式相减得：
Sn=1 2
+2(3 2
+1 22
+…+1 23
)-1 2n
，（10分）2n+1 2n+1
所以Sn=5-
．（12分）2n+5 2n