已知动点P在椭圆x225+y216=1上，点M在圆C2：（x-3）2+y2=1上_爱下问搜题

搜题请搜索小程序“爱下问搜题”

问题填空题

已知动点P在椭圆

x2

25

+

y2

16

=1上，点M在圆C₂：（x-3）²+y²=1上，点A（3，0）满足PM⊥AM，则|PM|的最小值为______．

答案

设点P（s，t），则

s2

25

+

t2

16

=1，可得t2=16-

16s2

25

，s∈[-5，5]．

∵PM⊥AM，∴|PM|²=|PA|²-|AM|²=（s-3）²+t²-1=s2-6s+8+16-

16s2

25

=

9

25

(s-

25

3

)2-1，

∵上述二次函数在s∈[-5，5]内单调递减，因此当s=5时，|PM|²取得最小值=3，即|PM|的最小值为

3

．

故答案为

3

．

单项选择题

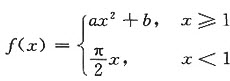函数，在x=1处可导，则（）。

A.A

B.B

C.C

D.D

单项选择题

某投资者以100元的价格平价购买了年息为8%，每年付息一次的债券，持有2年以后，以106元的价格卖出，那么该投资者持有期收益率（）。

A.11%

B.10.85%

C.13.33%

D.10%