问题
解答题
已知椭圆C:
(1)求椭圆C的方程; (2)从定点M(0,2)任作直线l与椭圆C交于两个不同的点A、B,记线段AB的中点为P,试求点P的轨迹方程. |
答案
(1)∵椭圆C:
+x2 a2
=1(a>b>0)的离心率e=y2 b2
,短轴长为21 2
,3
∴
,解得a=2,b=
=c a 1 2 2b=2 3 a2=b2+c2
,3
∴椭圆方程为
+x2 4
=1.y2 3
(2)设P(x,y),A(x1,y1),B(x2,y2),
若直线l与x轴垂直,则P(0,0);
若直线l与x轴不垂直,设直线l的方程为y=kx+2,k≠0.
由
,得(3+4k2)x2+16kx+4=0,…①
+x2 4
=1y2 3 y=kx+2
则
,将其消去k,得2x=x1+x2= -16k 3+4k2 y=kx+2
+(y-1)2=1,3x2 4
由①中△=(-16k)2-16(3+4k2)>0,解得k2>
,1 4
则x=
=-8k 3+4k2
∈[--8 4k+ 3 k
,0)∪(0,2 3 3
],y=2 3 3
+2=-8k2 3+4k2
∈(0,6 3+4k2
).3 2
综上,所求点P的轨迹方程为
+(y-1)2=1.y∈[0,3x2 4
).3 2

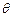 角,则:
角,则:
 是多少?
是多少?