（Ⅰ）把右焦点（c，0）代入直线x+y-

3

=0得c+0-

3

=0，解得c=

3

．

设A（x₁，y₁），B（x₂，y₂），线段AB的中点P（x₀，y₀），

则

x 21

a2

+

y 21

b2

=1，

x 22

a2

+

y 22

b2

=1，相减得

x 21 - x 22

a2

+

y 21 - y 22

b2

=0，

∴

x1+x2

a2

+

y1+y2

b2

×

y1-y2

x1-x2

=0，

∴

2x0

a2

+

2y0

b2

×(-1)=0，又kOP=

1

2

=

y0

x0

，

∴

1

a2

-

1

2b2

=0，即a²=2b²．

联立得

a2=2b2 a2=b2+c2 c= 3

，解得

b2=3 a2=6

，

∴M的方程为

x2

6

+

y2

3

=1．

（Ⅱ）∵CD⊥AB，∴可设直线CD的方程为y=x+t，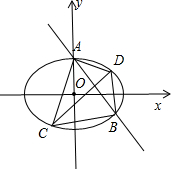

联立

y=x+t x2 6 + y2 3 =1

，消去y得到3x²+4tx+2t²-6=0，

∵直线CD与椭圆有两个不同的交点，

∴△=16t²-12（2t²-6）=72-8t²＞0，解-3＜t＜3（*）．

设C（x₃，y₃），D（x₄，y₄），∴x3+x4=-

4t

3

，x3x4=

2t2-6

3

．

∴|CD|=

(1+12)[(x3+x4)2-4x3x4]

=

2[(- 4t 3 )2-4× 2t2-6 3 ]

=

2 2 • 18-2t2

3

．

联立

x+y- 3 =0 x2 6 + y2 3 =1

得到3x²-4

3

x=0，解得x=0或

4

3

3

，

∴交点为A（0，

3

），B(

4

3

3

，-

3

3

)，

∴|AB|=

( 4 3 3 -0)2+(- 3 3 - 3 )2

=

4 6

3

．

∴S_{四边形ACBD}=

1

2

|AB||CD|=

1

2

×

4 6

3

×

2 2 • 18-2t2

3

=

8 3 • 18-2t2

9

，

∴当且仅当t=0时，四边形ACBD面积的最大值为

8

3

6

，满足（*）．

∴四边形ACBD面积的最大值为

8

3

6

．