由均值不等式

1=

1

m

+

2

n

≥2

1 m • 1 n

，

当且仅当

1

m

=

2

n

时等号成立，

也就是

1

m

=

2

n

=

1

2

，

所以m=2，n=4．

∵

x|x|

m

+

y|y|

n

=1，

∴

x|x|

2

+

y|y|

4

=1．

①当x＞0，y＞0，

表示

x2

2

+

y2

4

=1的椭圆；

②当x＞0，y＜0，

表示

x2

2

-

y2

4

=1以x轴为实轴的双曲线；

③当x＜0，y＞0，

表示

y2

4

-

x2

2

=1以y轴为实轴的双曲线；

④当x＜0，y＜0，

表示-

x2

2

-

y2

4

=1，

因为左边恒≤0所以不可能=右边，

所以此时无解．

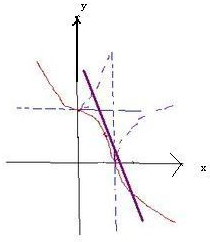
所以如图得到图象，

结合图象知直线y=-

2

x+2与曲线

x|x|

m

+

y|y|

n

=1交点个数是2个．

故答案为：2．