问题
填空题
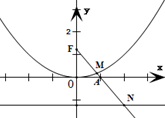
已知点A(1,0),抛物线x2=4y的焦点为F,射线FA与抛物线相交点M,与其准线交于N,则|FM|:|MN|=______.
答案
∵抛物线x2=4y的焦点为F(0,1),
∴直线AF的斜率为k=
=-1,1-0 0-1
可得直线AF的方程为y=-(x-1),即y=-x+1.
由
消去y,得x2+4x-4=0,解得x=-2±2y=-x+1 x2=4y
.2
∵射线FA与抛物线相交点M,∴M的横坐标为xM=-2+2
,2
又∵抛物线x2=4y的准线为y=-1,
∴联解
,得y=-x+1 y=-1
,所以射线FA与抛物线的准线相交于点N(2,-1),x=2 y=-1
由此可得|FM|:|FN|=xM:xN=(-2+2
):2=2
-1,2
∴|FM|=(
-1)|FN|,|FN|=(2
+1)|FM|,2
可得|MN|=|FN|-|FM|=
|MN|,所以|FM|:|MN|=2
.2 2
故答案为:2 2