问题
填空题
若直线y=kx+2与曲线y=
|
答案
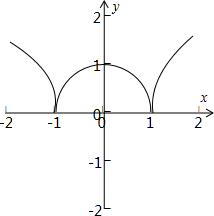
曲线y=
对应的函数图象如图所示.
,|x|>1x2-1
,|x|≤11-x2
当直线y=kx+2与半圆相切时,k=±
满足题意;3
当直线y=kx+2过(±1,0)时,k=±2满足题意;
|x|>1时,y=
为双曲线在x轴上方的部分,其渐近线为y=±x.x2-1
故当直线y=kx+2与渐近线平行时,k=±1,
∴-1<k<1时,直线与双曲线有两个不同的交点,
∴k∈{k|-1<k<1,或k=±
,或k=±2}.3
故答案为:{k|-1<k<1,或k=±
,或k=±2}.3