设a∈R,函数f(x)=x2+ax+4.(1)解不等式f(x)+f(-x)<10x;(2)求f(x)在区间[1,2]上的最小值g(a).
(1)f(x)+f(-x)<10x,即2x2+8<10x,…(2分)
化简整理得x2-5x+4<0,解得1<x<4.…(4分)
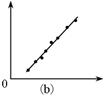
(2)函数f(x)=x2+ax+4图象的对称轴方程是x=-
.a 2
①当-
≤1,即a≥-2时,f(x)在区间[1,2]上单调递增,所以f(x)min=f(1)=a+5; …(6分)a 2
②当1<-
<2,即-4<a<-2时,f(x)在区间[1, -a 2
]上单调递减,在[-a 2
, 2]上单调递增所以,f(x)min=f(-a 2
)=4-a 2
; …(8分)a2 4
③当-
≥2,即a≤-4时,f(x)在区间[1,2]上单调递减,所以f(x)min=f(2)=2a+8.a 2
综上,g(a)=
…(10分)a+5,a≥-2 4-
,-4<a<-2a2 4 2a+8,a≤-4.


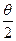 )],式中T0为摆角趋近于0°时的周期,a为常数;为了用图象法验证该关系式,需要测量的物理量有________;某同学在实验中得到了如图(b)所示的图线,则图线的斜率表示_______。
)],式中T0为摆角趋近于0°时的周期,a为常数;为了用图象法验证该关系式,需要测量的物理量有________;某同学在实验中得到了如图(b)所示的图线,则图线的斜率表示_______。