问题
问答题
设随机变量X服从参数为λ(λ＞0)的泊松分布，从总体X中抽取简单随机样本X1，X2，…，Xn。
(Ⅰ)推导统计量
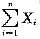的概率分布；
(Ⅱ)证明：
是θ=λ2的一个无偏估计量．
答案
参考答案：由于X1，X2，…，Xn相互独立，都服从参数为λ的泊松分布，因此T2=X1+X2的所有可能取的值为0，1，2，…，且
[*]
即T2=X1+X2服从参数为2λ的泊松分布．
对于2＜l＜n，设Tl=X1+X2+…+Xl服从参数为lλ，的泊松分布，则Tl与Xl+1相互独立，Tl+1的
所有可能取的值为0，1，2，…，且
[*]
即Tl+1=X1+X2+…+Xl+1服从参数为(l+1)λ的泊松分布，因此[*]服从参数为nλ的泊松分布．
证：(Ⅱ)因为
[*]
所以
[*]
即[*]是θ=λ2的一个无偏估计量．
解析：
[分析]： 记Tj=X1+X2+…+Xj，j=2，3，…，n．根据X1，X2，…，Xn相互独立，都服从参数为λ的泊松分布，可得Tn服从参数为nλ的泊松分布，E(Tn)=nλ，[*][E(Tn)]2-E(Tn)}=λ2．