问题
问答题
解放军空军某部伞兵在某次军事演习中做低空跳伞演习,当飞机离地面224m 时,伞兵离开飞机在竖直方向做自由落体运动.运动一段时间后,立即打开降落伞,展伞后伞兵以12.5m/s2的平均加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5m/s.g=10m/s2.
求:(1)伞兵展伞时,离地面的高度至少为多少?着地时相当于从多高处自由落下?
(2)伞兵在空中的最短时间.
答案
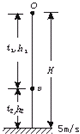
作出在竖直方向上的运动情况如图所示
(1)由公式ν2-ν02=2ax可得
第一阶段伞兵做自由落体运动:ν2=2gh1①
第二阶段伞兵做匀减速直线运动,v末=5m/s,加速度a=-12.5m/s2:ν末2-ν2=2ah2②
又:h1+h2=H③
解①②③式可得展伞时离地面的高度至少为h2=99 m.
设以ν1=5m/s速度着地相当于从高h′处自由下落.则h/=
=ν 21 2g
=1.25m52 2×10
(2)由公式x=ν0t+
at2可得:1 2
第一阶段:h1=
gt121 2
解得:t1=5s
第二阶段:h2=νt2-
a1 2 t 22
解得:t2=3.6m/s
又:t=t1+t2=8.6s
所以伞兵在空中的最短时间为t=8.6s.
