（1）设P（x，y），由已知得

y

x+2

•

y

x-2

=-

3

4

(x≠±2)

化简得

x2

4

+

y2

3

=1，

所以点P的轨迹方程为

x2

4

+

y2

3

=1（x≠±2）．------------（3分）

（2）解法1：设点P（x₀，y₀），PB的中点为Q，则Q(

x0+1

2

，

y0

2

)，|PB|=

(x0-1)2+ y 20

=

x 20 -2x0+1+3- 3 4 x 20

=

1 4 x 20 -2x0+4

=2-

1

2

x0，

即以PB为直径的圆的圆心为Q(

x0+1

2

，

y0

2

)，半径为r1=1-

1

4

x0，

又圆x²+y²=4的圆心为O（0，0），半径r₂=2，|OQ|=

( x0+1 2 )2-( y0 2 )2

=

1 4 x 20 + 1 2 x0+ 1 4 + 1 4 (3- 3 4 x 20 )

=

1 16 x 20 + 1 2 x0+1

=1+

1

4

x0，

故|OQ|=r₂-r₁，即两圆内切．------------------（7分）

解法2：由椭圆的定义得|PM|+|PN|=2a=4

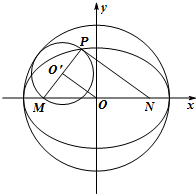
圆心距|OO′|=

1

2

|PN|=2-

1

2

|PM|=2-|O′M|

所以以PB为直径的圆与圆x²+y²=4内切．

（3）解法1：

若直线PN的斜率不存在，则PN：x=-1，解得P(-1，

3

2

)，N(-1，-

3

2

)，|PN|=3，S△PON=

3

2

；

若直线PN的斜率存在，设直线PN的方程为y=k（x+1）（k≠0），

由

y=k(x+1) x2 4 + y2 3 =1

得（4k²+3）x²+8k²x+4k²-12=0，

设P（x₁，y₁），N（x₂，y₂），△=64k⁴-4（4k²+3）（4k²-12）=144（k²+1），|PN|=

1+k2

|x1-x2|=

1+k2

△

4k2+3

=

12(1+k2)

4k2+3

，

原点O到直线PN的距离d=

|k|

1+k2

，

所以S△PON=

1

2

|PN|d=

6 1+k2 |k|

4k2+3

=6

k2+k4 (4k2+3)2

设4k²+3=t，则t＞3，则有S△PON=6

- 3 16t2 - 1 8t + 1 16

=6

- 3 16 ( 1 t + 1 3 )2+ 1 12

因为0＜

1

t

＜

1

3

，所以S△PON∈(0，

3

2

)．

综上所述，S_△PON的最大值为

3

2

．------------------（12分）

解法2：设直线PN的方程为x=my-1．

由

x=my-1 x2 4 + y2 3 =1

得（3m²+4）y²-6my-9=0，

设P（x₁，y₁），N（x₂，y₂），△=144（m²+1），|y1-y2|=

△

3m2+4

=

12 m2+1

3m2+4

，S△PON=

1

2

|OM||y1-y2|=

6 m2+1

3m2+4

=6

m2+1 (3m2+4)2

设3m²+4=t，则t≥4，则有S△PON=6

t-1 3t2

=6

- 1 3 ( 1 t - 1 2 )2+ 1 12

．

因为0＜

1

t

≤

1

4

，所以当

1

t

=

1

4

，即t=4，m=0时，S_△PON的最大值为

3

2

．------------------（12分）