（1）法一：依题意，设椭圆方程为

y2

a2

+

x2

b2

=1(a＞b＞0)，则2c=2

3

，c=

3

，

∵椭圆两个焦点为F1(0，-

3

)，F2(0，

3

)，∴2a=|MF₁|+|MF₂|=

(- 13 4 )2+( 3 2 + 3 )2

+

(- 13 4 )2+( 3 2 - 3 )2

=4，∴a=2．

∴b²=a²-c²=1，∴椭圆C的方程为

y2

4

+x2=1．

法二：依题意，设椭圆方程为

y2

a2

+

x2

b2

=1(a＞b＞0)，则

2c=2 3 ( 3 2 )2 a2 + (- 13 4 )2 b2 =1

，即

a2-b2 = 3 3 4a2 + 13 16b2 =1

，解之得

a=2 b=1

，

∴椭圆C的方程为

y2

4

+x2=1．

（2）法一：设A、B两点的坐标分别为（x₁，y₁），（x₂，y₂），则

x1+x2

2

=

1

2

，

y1+y2

2

=1，

y12

4

+x12=1…①

y22

4

+x22=1…②

①-②，得

y12-y22

4

+x12-x22=0，

∴kAB=

y1-y2

x1-x2

=

-(x1+x2)

y1+y2 4

=

-1

2 4

=-2，

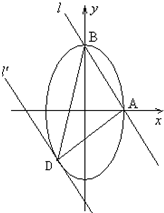
设与直线AB平行且与椭圆相切的直线方程为l'：2x+y+m=0，

联立方程组

y2 4 +x2=1 2x+y+m=0

，消去y整理得8x²+4mx+m²-4=0，

由判别式△=16m²-32（m²-4）=0得m=±2

2

，

由图知，当m=2

2

时，l'与椭圆的切点为D，此时△ABD的面积最大，

∵m=2

2

，∴x_D=-

m

4

=-

2

2

，yD=-

2

．

∴D点的坐标为(-

2

2

，-

2

)．

法二：设直线AB的方程为y-1=k(x-

1

2

)，联立方程组

y2 4 +x2=1 y-1=k(x- 1 2 )

，

消去y整理得(k2+4)x2-(k2-2k)x+

1

4

k2-k-3=0，

设A、B两点的坐标分别为（x₁，y₁），（x₂，y₂），则x1+x2=

k2-2k

k2+4

=1，∴k=-2．

∴直线AB的方程为y-1=-2(x-

1

2

)，即2x+y-2=0．

（以下同法一）．