问题
选择题
(A题)已知点P是圆x2+y2=4上一动点,直线l是圆在P点处的切线,动抛物线以直线l为准线且恒经过定点A(-1,0)和B(1,0),则抛物线焦点F的轨迹为( )
A.圆
B.椭圆
C.双曲线
D.抛物线
答案
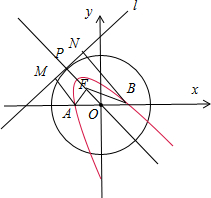
如图所示,
过点A、B分别作AM⊥l,BN⊥l,垂直为M,N.
根据抛物线的定义可得:|AF|=|AM|,|BF|=|BN|,
∴|AF|+|BF|=|AM|+|BN|.
连接OP,则OP⊥l,∴AM∥OP∥BN,
∵O是线段AB的中点,∴OP是梯形ABNM的中位线,
∴|AF|+|BF|=2|OP|=4>2=|AB|,
∴根据椭圆的定义可得,点F的轨迹是以点A,B为焦点,2a=4为长轴长的椭圆.
故选B.