问题
解答题
过双曲线
求:(1)|AB|的值; (2)△F1AB的周长(F1为双曲线的左焦点). |
答案
(1)由双曲线方程
-y2=1可得a=x2 3
,b=1,3
又由c2=a2+b2,得c=2,F2(2,0)所以直线AB的方程为:y=x-2 设A(x1,y1)、B(x2,y2) 由
消去y得2x2-12x+15=0y=x-2
-y2=1x2 3 ∴x1+x2=6,x1x2= 15 2 由弦长公式|AB|=
•1+k2
,得(x1+x2)2-4x1x2 |AB|=
•1+12
=262-4× 15 2 3
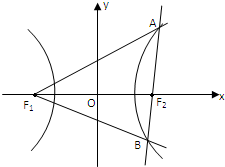
(2)如图,由双曲线定义得:
|AF1|=|AF2|+2a,
|BF1|=|BF2|+2a
∴△F1AB的周长=|AF1|+|BF1|+|AB|
=|AF1|+|BF2|+4×
+|AB|3
=2|AB|+4
=83 3