问题
选择题
已知{an}是递减等比数列,a2=2,a1+a3=5,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是( )
|
答案
(a2)2=a1•a3=4,a1+a3=5,
∴a1和a3是方程x2-5x+4=0的两个根,解得x=1或4
∵{an}是递减等比数列,∴a1>a3,
∴a1=4,a3=1
∴q2=
=a3 a1 1 4
∵{an}是递减等比数列,∴q>0
∴q=1 2
∴Sn=a1a2+a2a3+…+anan+1=a12q+a12q3+a12q5…+a12q2n-1=
=8[1-(
)n]1 4 1- 1 4
(1-32 3
)<1 4n 32 3
∵{an}是递减等比数列,
∴{Sn}的最小项为S1=8
∴a1a2+a2a3+…+anan+1(n∈N*)的取值范围是[8,
)32 3
故选C

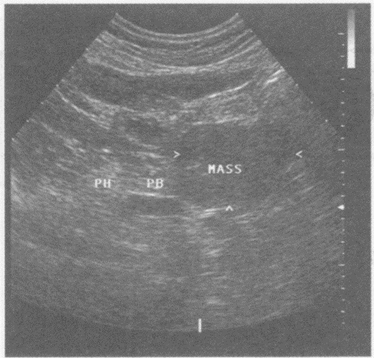
 超声提示()
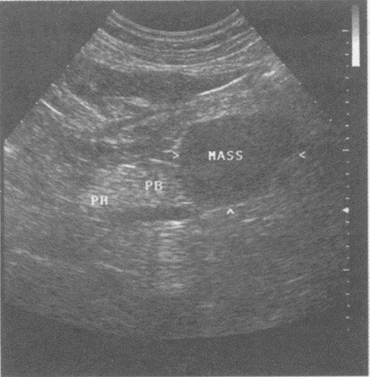
超声提示()