问题
问答题
设随机变量X的概率密度为
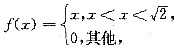
随机变量Y=max(X,X2),求:
(Ⅰ)Y的分布函数FY(y)及概率密度fY(y);
(Ⅱ)Y的数学期望E(Y);
(Ⅲ)X与Y的协方差Cov(X,Y).
答案
参考答案:记Y=g(X),则
[*]
当y<0时,FY(y)=0;
当y≥2时,FY(y)=1;
当0≤y<1时,有
[*]
当1≤y<2时,有
FY(y)=P{Y≤y}=P{0<X<1)+P{1≤X2≤y)
[*]
综合上述讨论,得
[*]
(Ⅱ)解法一 根据数学期望的定义,有
[*]
解法二 根据计算随机变量函数的数学期望的公式,有
[*]
(Ⅲ) 由于
[*]
Cov(X,Y)=E(XY)-E(X)E(Y)
[*]
解析:
[分析]: Y是X的函数,记为g(X),则
[*]
可按照y的不同取值求得FY(y)=P{Y≤y
