问题
解答题
已知椭圆C1:
|
答案
设直线方程是
(t是参数),分别代入椭圆、抛物线方程得:x=1+
t1 2 y=
t3 2
5t2+4t-12=0(1)3t2-4pt-8p=0(2)
设A、B、C、D的参数分别为t1、t2、t3、t4,
则|AB|=|t1-t2|=
,|CD|=|t3-t4|=4 p2+6p 3
,由|AB|:|CD|=5:3解得p=2.16 5
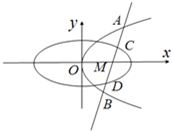
已知椭圆C1:
|
设直线方程是
(t是参数),分别代入椭圆、抛物线方程得:x=1+
t1 2 y=
t3 2
5t2+4t-12=0(1)3t2-4pt-8p=0(2)
设A、B、C、D的参数分别为t1、t2、t3、t4,
则|AB|=|t1-t2|=
,|CD|=|t3-t4|=4 p2+6p 3
,由|AB|:|CD|=5:3解得p=2.16 5
